Shortest way to find Fibonacci sequence in JavaScript?

Let's first take a look at how the Fibonacci sequence looks like, in case you haven't seen it before:

$$ 0, 1, 1, 2, 3, 5, 8, 13, \ldots $$

The first two terms are $0$ and $1$. Any other term is the sum of previous two terms. Very simple right!

There are many different ways to generate this sequence. Today I will share with you the one that I figured out myself. My goal was to find shortest possible way to do it. I'm not sure if it is the one!

Here it goes:

const fibSeq = (n) =>
  n < 2 ? [[0], [0, 1]][n] : ((s) => [...s, s.pop() + s.pop()])(fibSeq(n - 1));

console.log(fibSeq(10));

The output is:

[0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55];

Looking at that cryptic line, some of you might be thinking of me as some sort of genius, but I'm not. It took me an embarrassingly long time to craft this line. And even after solving it, I needed some more time to actually understand how it works.

I'm not here to preach about clever coding. Applying code-fu in real-world projects may not be appreciated by others, including your future self. Save it for the fun moments. Enough with the advice—let's dive into the breakdown of how it actually works!

The above code is actually two functions mashed up together. Let's first seperate them:

const addNextTerm = (seq) => [...seq, seq.pop() + seq.pop()];

const fibSeq = (n) => (n < 2 ? [[0], [0, 1]][n] : addNextTerm(fibSeq(n - 1)));

console.log(fibSeq(10));

Let's make it more clear by using if/else instead of the ternary operator and not making clever use of pop() method of arrays.

const addNextTerm = (seq) => [
  ...seq,
  seq[seq.length - 2] + seq[seq.length - 1],
];

const fibSeq = (n) => {
  if (n == 0) {
    return [0];
  } else if (n == 1) {
    return [0, 1];
  } else {
    return addNextTerm(fibSeq(n - 1));
  }
};

console.log(fibSeq(10));

In this version of fibSeq, the addNextTerm gives us the same result except the fact that it doesn't mutates its input which pop() did in the previous version of our code. Also note that mutating the input worked fine, since what we needed was the return value.

Now there is no magic except recursion. If I struggle with writing recursive code, I remind myself this thinking model:

Figure out the recursive pattern. Then handle the cases that this pattern can't handle.

This way never disappointed me.

The hardest part is figuring out the recursive pattern.

Here, for getting the Fibonacci sequence of first $n$ terms where $n \gt 1$, is the same as getting the Fibonnaci sequence of first $n - 1$ terms and then add an extra term in it. Notice how the idea “getting Fibonacci sequence of first $n$ terms where $n \gt 1$” involves itself. So this a recursive pattern. In the above code this pattern is in the else block.

In the above code the if and else if blocks handle cases where the recursive pattern doesn't make sense.

Flowing with the control flow that happens inside a recursive algorithm is like going down the rabbit hole and emerging with the result. Sometimes, practicing this allows you to gain a better understanding of how the computer interprets your recursive code. Figure 1 illustrates this control flow for a fibSeq(3) call.

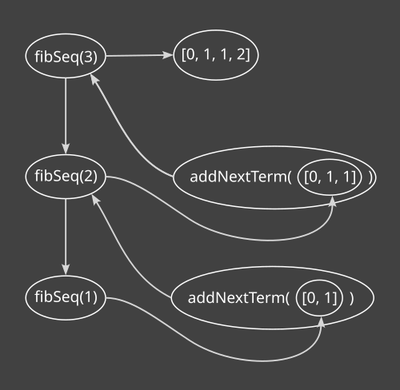
I hope you found this article interesting. Thanks for reading!

Bonus: Generating LARGE numbers

The Number type can't accurately calculate very large integers. Why not leverage BigInt for some more fun?

const fibSeq = (n) =>
  n < 2n
    ? [[0n], [0n, 1n]][n]
    : ((s) => [...s, s.pop() + s.pop()])(fibSeq(n - 1n));

console.log(fibSeq(1000n).map((t, i) => `${i} 👉 ${t}`).join`\n`);